ПРЕДИСЛОВИЕ
По сложившейся на кафедре прикладной математики и информационных технологий ДВГУ традиции студентам-первокурсникам читается вводный курс из 9-10 лекций по специальности 06.18.00 – “математические методы в экономике”. Цель курса – показать слушателям на простых содержательных примерах суть их будущей профессии и заложить основы будущего профессионального мировоззрения. Одновременно намечаются истоки и идейная связь ряда специальных дисциплин (линейное и нелинейное программирование, теория игр, исследование операций, теория выбора и принятия решений), с которыми студенты, будут знакомиться позже, на старших курсах. Изложение материала строится на базе школьной программы по математике и вполне доступно старшеклассникам. Для самостоятельной проверки знаний в конце каждого раздела приведены вопросы, упражнения и тестовые задания с ответами.
Под исследованием операций понимается научный подход к решению задач организационного управления [1]. Термин “исследование операций” возник в годы второй мировой войны и означал первоначально планирование боевых операций. В современной более общей трактовке – это научная методология и технология нахождения рационально обоснованных решений в различных областях человеческой деятельности. Исследование операций охватывает вопросы построения математических моделей ситуаций, определения наилучших решений и их нахождения, анализа и практического применения.
Тестовым заданиям, компьютерной верстке и удобствам электронной версии пособие обязано Ларисе Яковлевне Ащепковой. Большая работа по размещению пособия на сайте проделана Евгением Викторовичем Полковниковым. Выражаю им свою искреннюю признательность и благодарность.
Автор
Чтобы составить первое представление о предмете, рассмотрим несколько типовых задач исследования операций.
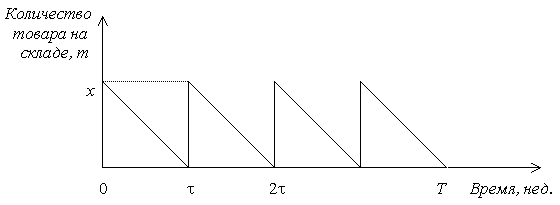
 Пример 1.1. Задача управления запасами [1]. На складе хранится товар, которым обеспечивается сеть магазинов. Товар поступает на склад равными порциями через равные промежутки времени и расходуется с постоянной скоростью так, что к моменту очередного поступления его запасы становятся равными нулю (рис 1.1).
Пример 1.1. Задача управления запасами [1]. На складе хранится товар, которым обеспечивается сеть магазинов. Товар поступает на склад равными порциями через равные промежутки времени и расходуется с постоянной скоростью так, что к моменту очередного поступления его запасы становятся равными нулю (рис 1.1).
Известны:
с1 - стоимость доставки одной порции товара ( руб.),с2 - стоимость хранения тонны товара в течение недели (руб./(т х нед.)),
τ - время между двумя последовательными поступлениями товара (нед.),
Т - время обслуживания сети магазинов (плановый период, нед.),
N - необходимое количество товара в течение планового периода (спрос, т).
Требуется определить количество товара в порции так, чтобы общие затраты на обеспечение спроса N и хранение товара за время Т были минимальными.
Перейдем к математической формулировке задачи. Обозначим через х искомое количество товара в порции (в тоннах). Подсчитаем отдельно затраты на доставку и хранение товара. На покрытие спроса N необходимо N/x доставок товара, затраты на которые (в руб.) составят
с1 N/x. (1.1)
За τ недель (между двумя последовательными поставками) запасы товара на складе убывают с постоянной скоростью от x т до 0, поэтому средний запас составит 0.5x т.
Действительно, если бы товар не расходовался, то затраты на хранение за τ недель равнялись бы с2x τ руб., т.е. были пропорциональны площади xτ прямоугольника со сторонами x и τ (см. рис. 1.1). При равномерном расходовании товара затраты пропорциональны площади 0.5xτ прямоугольного треугольника с катетами x и τ, которая ровно в два раза меньше площади соответствующего прямоугольника. Следовательно, затраты (в руб.) на хранение товара в течение планового периода равны
с2 (0.5x τ )( N /x). (1.2)
Складывая затраты (1.1) и (1.2), получим формулу общих затрат
Поскольку здесь τ (N /x) = Т, то окончательно получим
З(х) = с1 N /x +0.5 с2Т x. (1.3)
Итак, математически задача управления запасами заключается в нахождении такого положительного значения неизвестной х, при котором функция общих затрат (1.3) имеет минимум. В символической записи
З(х) = с1 N /x +0.5 с2 Т x → min, (1.4)
х > 0. (1.5)
Условие (1.4) задачи называют целевым, оно содержит требование (минимизации целевой функции), по которому находится искомое x. Условие (1.5), вытекающее из физического смысла неизвестной x, есть ограничение на x.
Задача управления запасами, содержащая ограничение на неизвестную х, относится к классу задач на условный экстремум. Конечно, здесь она предельно упрощена. Существуют более сложные постановки, которые учитывают нерегулярность поставок товара, ограниченную емкость склада и другие факторы. По образному выражению Г. Вагнера [1] задача управления запасами "играет в исследовании операций такую же роль, как законы Ньютона в физике".

 Пример
1.2. Проблема" двух картошек" [1]. Фирма по переработке картофеля производит три вида продукции:
картофельные дольки, кубики и хлопья. Анализ загруженности оборудования и спроса на рынке
показывает возможность произвести и сбыть до 1.8 т долек, 1.2 т кубиков и 2.4 т хлопьев. Необходимый для переработки картофель фирма закупает у двух поставщиков. Количество готовой продукции и относительная прибыль (доход от реализации готовой продукции за вычетом стоимости сырья), которые можно получить из одной т картофеля каждого поставщика, указаны в табл. 1.1.
Пример
1.2. Проблема" двух картошек" [1]. Фирма по переработке картофеля производит три вида продукции:
картофельные дольки, кубики и хлопья. Анализ загруженности оборудования и спроса на рынке
показывает возможность произвести и сбыть до 1.8 т долек, 1.2 т кубиков и 2.4 т хлопьев. Необходимый для переработки картофель фирма закупает у двух поставщиков. Количество готовой продукции и относительная прибыль (доход от реализации готовой продукции за вычетом стоимости сырья), которые можно получить из одной т картофеля каждого поставщика, указаны в табл. 1.1.
| Вид готовой продукции | Выход готовой продукции из 1 т картофеля, т | Потребности рынка сбыта, т | |
| Поставщик 1 | Поставщик 2 | ||
| Дольки | 0.2 | 0.3 | 1.8 |
| Кубики | 0.2 | 0.1 | 1.2 |
| Хлопья | 0.3 | 0.3 | 2.4 |
| Относительная прибыль, ден. ед. | 5.0 | 6.0 | |
Требуется определить, какое количество картофеля надо приобрести у каждого поставщика, чтобы обеспечить наибольшую относительную прибыль с учетом возможности сбыта готовой продукции.
Перейдем от содержательного описания ситуации к формализованному. Введем неизвестные х1 и х2 - количество картофеля (т), закупаемого у поставщиков 1 и 2 соответственно. Используя три первые строки таблицы, составим балансовые соотношения
В левой части каждого неравенства записан выход готовой продукции из закупленного картофеля, а в правой части – предельные потребности в продукции на рынке сбыта. Физические размерности сравниваемых величин в балансовых соотношениях одни и те же – т. Относительная прибыль П подсчитывается с помощью последней строки таблицы и в ден. ед. равна
По смыслу задачи необходимо найти такие значения неизвестных х1 и х2, которые обеспечивают максимальную относительную прибыль
П (х1, х2) = 5х1 + 6х2 → mах (1.6)
и удовлетворяют ограничениям типа неравенства (балансовым соотношениям для долек, кубиков и хлопьев)
0.2х1 + 0.3х2 ≤ 1.8, (1.7)
0.2х1 + 0.1х2 ≤ 1.2, (1.8)
0.3х1 + 0.3х2 ≤ 2.4, (1.9)
х1 ≥ 0, х2 ≥ 0. (1.10)
Условия неотрицательности (1.10) добавлены к балансовым соотношениям (1.7) - (1.9), исходя из физического смысла неизвестных.
Полученная задача называется задачей линейного программирования. Отличительная ее особенность состоит в линейности всех функций, задающих целевое условие (1.6), ограничения (1.7) - (1.9) и условия неотрицательности (1.10).

Математическая постановка задачи достаточно очевидна. В принятых обозначениях общая стоимость С изготовления продукции равна
и требование выполнения заказа приводит к условию х1 + х2 = а. Необходимо найти такие значения неизвестных х1 и х2 , которые доставляют минимум функции
С (х1, х2) = х12/с1 + х22/с2 → min (1.11)
при ограничениях
х1 + х2 = а, х1 ≥ 0, х2 ≥ 0. 12)
Неравенства (1.12) отражают физический смысл неизвестных. Целевая функция (1.11) в задаче квадратичная относительно х1, х2, поэтому ее относят к задачам нелинейного (квадратичного) программирования.

Здесь мы сталкиваемся с конфликтной ситуацией, в которой интересы двух участников противоположны. Займемся ее математической формализацией. Для этого нам придется решить довольно деликатный вопрос об оценке жизни Шерлока Холмса. Не вдаваясь в дискуссию, условимся оценить ее в 100 условных единиц (предоставив, конечно, самому Шерлоку Холмсу решить вопрос об эквиваленте условной единицы).
У каждого участника конфликта есть два способа действия: сойти с поезда в Дувре или в Кентербери. Мы будем обозначать их через К и Д соответственно. В теории игр участников конфликтной ситуации называют игроками, а их возможные действия в конфликте – стратегиями. Следовательно, К и Д в данном случае – стратегии игроков.
Выбирая свои стратегии независимо, игроки создают в игре четыре возможные ситуации: КК, КД, ДК, ДД. Если считать Шерлока Холмса первым игроком, а профессора Мориарти. – вторым, то ситуация КД, например, означает, что Шерлок Холмс сходит с поезда в Кентербери и Мориарти – в Дувре. В этой ситуации Шерлок Холмс считал бы свою жизнь наполовину спасенной, т.е. получил бы в качестве выигрыша 50 условных единиц. Его выигрыши в остальных ситуациях КК, ДК, ДД составят соответственно - 100, 100, - 100 условных единиц. Отрицательный выигрыш трактуется как проигрыш.
Для наглядности удобнее представить выигрыши Шерлока Холмса табл.1.2. По существу она и есть формализованное описание конфликтной
| Стратегии Мориарти | |||
| К | Д | ||
| Стратегии Шерлока Холмса | К | -100 | 50 |
| Д | 100 | -100 | |
ситуации. Хотя в таблице указаны только выигрыши первого игрока, выигрыши второго определяются автоматически. Он выигрывает ровно столько, сколько проигрывает первый игрок. Таким образом, независимо от ситуации сумма выигрышей игроков равна нулю.
Задача состоит в нахождении таких стратегий, при которых выигрыш первого игрока максимален и проигрыш второго игрока минимален.
По понятным соображениям приведенная игра называется антагонистической игрой двух лиц с нулевой суммой выигрышей.

Выигрыши Студента
| Стратегии Преподавателя | |||
| + | - | ||
| Стратегии Студента | Х | 2 (оценили по заслугам) |
-1 (обидно) |
| П | 1 (удалось словчить) |
0 (получил по заслугам) |
|
По поводу оценок морального удовлетворения, указанных в таблицах, могут быть разные мнения. Например, некоторые студенты считают, что выигрыш Студента в 1 балл в ситуации, когда он выбрал стратегию П, а Преподаватель – стратегию +, явно занижен. Не вдаваясь в полемику, которая неизбежно затронула бы вопросы нравственности и воспитания молодежи, отметим, что проблема соответствия (адекватности) математической модели и моделируемого явления, безусловно, есть, и о ней мы будем говорить позже.
Игра, заданная таблицами 1.13, 1.14, называется биматричной. Она состоит в нахождении таких стратегий, которые обеспечивают игрокам максимальные выигрыши.
| Стратегии Преподавателя | |||
| + | - | ||
| Стратегии Студента | Х | 0 (все нормально) |
-2 (проявил несправедливость) |
| П | -3 (дал себя обмануть) |
-1 (студент придет еще раз) |
|
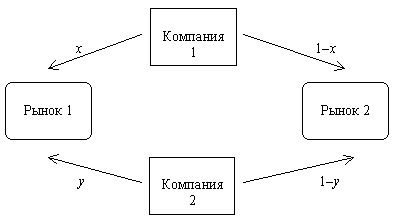
 Пример 1.6. Борьба за рынки [3]. Две компании, производящие одну и ту же продукцию, конкурируют на двух рынках сбыта. Каждая из них может распределить свою продукцию между рынками в любых долях. Считается, что компания, сумевшая создать на рынке долевое превосходство своей продукции, получит доход, пропорциональный разности долей своей и конкурентной продукции. В противном случае она несет убыток, подсчитываемый по то же правилу. Спрашивается, как каждая компания должна распределять свою продукцию между рынками, чтобы получить наибольший доход.
Пример 1.6. Борьба за рынки [3]. Две компании, производящие одну и ту же продукцию, конкурируют на двух рынках сбыта. Каждая из них может распределить свою продукцию между рынками в любых долях. Считается, что компания, сумевшая создать на рынке долевое превосходство своей продукции, получит доход, пропорциональный разности долей своей и конкурентной продукции. В противном случае она несет убыток, подсчитываемый по то же правилу. Спрашивается, как каждая компания должна распределять свою продукцию между рынками, чтобы получить наибольший доход.
Для построения математической модели ситуации обозначим через х и у доли продукции, направляемые компаниями 1 и 2 соответственно на первый рынок (рис.1.2). Тогда доход Н11(х, у) компании 1 на первом рынке равен
где k11 – положительный коэффициент. Точно так же доход Н12(х, у) компании 1 на втором рынке составит
Здесь k12 - вообще говоря, другой (отличный от k11) положительный коэффициент. Очевидно, при х≥у компания на первом рынке имеет доход и на втором – убыток. Если же х≤у , то картина противоположная. Общий доход Н1(х, у) компании на двух рынках будет суммой Н11(х, у) и Н12(х, у), т.е.
Проводя такие же рассуждения, получим формулу общего дохода второй компании на двух рынках
где k21 , k22 – положительные коэффициенты.
По смыслу задачи требуется найти такие значения неизвестных х и у, которые доставляют максимум функциям доходности
Н1(х, у) = ( k11 – k12) (х – у) → mах, (1.13)
Н2(х, у) = ( k22 – k21) (х – у) → mах (1.14)
при условиях
0≤х≤1, 0≤у≤1. (1.15)
Неравенства (1.15) отражают физический смысл неизвестных. В приведенной игре каждый игрок имеет свою функцию выигрыша и действует независимо от другого. Игра является частным случаем бескоалиционной игры n лиц.
Вопросы и упражнения
-
Какие изменения в математической модели возникнут, если в условия задачи включить:
-ограничение на предельное количество товара в порции,
-требование иметь на складе резервный запас товара не менее установленного уровня. -
Согласованы ли размерности величин в формуле (1.4) общих затрат?
-
Можно ли утверждать, что при пропорциональном изменении стоимостей затрат и хранения функция общих затрат изменится пропорционально?
Проблема двух картошек -
Как изменятся балансовые соотношения для долек, хлопьев и кубиков, если фирма выполняет определенный заказ на готовую продукцию?
-
Как следует согласовать выпуск готовой продукции в предыдущем задании, чтобы обеспечить совместность условий задачи?
-
Повлияет ли на решение задачи пропорциональное изменение величин относительной прибыли в 2 раза, в 3 раза?
-
Какую дополнительную информацию надо для того, чтобы сформулировать задачу для трех поставщиков картофеля?
-
Какие дополнительные исходные данные нужны для расширения списка готовой продукции на одно наименование, два наименования?
Производственная задача "места и времени" -
Пусть в задаче речь идет о заказе на неделимые единицы продукции. Какие изменения появятся в математической модели?
-
Как отразится на математической постановке задачи ограничения на производственные мощности заводов?
-
Как должны быть согласованы ограничения на производственные мощности заводов-изготовителей продукции и величину заказа, чтобы условия задачи были совместны?
Преследование Шерлока Холмса -
Насколько вы согласны с оценками выигрышей Шерлока Холмса в разных ситуациях? Какие из оценок и как следовало бы, по вашему мнению, подкорректировать?
-
Какие психологические факторы учитывает или не учитывает математическая постановка игры?
-
Придумайте пример операции, которую можно было бы сформулировать в терминах матричной игры. Каковы в ней стратегии игроков, множества стратегий, выигрыши игроков в разных ситуациях?
Зачет -
Можно ли игру "Преследование Шерлока Холмса" сформулировать как биматричную? Как будет выглядеть таблица выигрышей профессора Мориарти?
-
Повлияет ли на решение биматричной игры 1) пропорциональное изменение всех элементов матриц выигрыша, 2) прибавление ко всем элементам матриц выигрыша одной и той же постоянной?
-
Можно ли утверждать, что класс биматричных игр содержит в себе класс матричных игр? Верно ли обратное утверждение?
Борьба за рынки -
Чем можно объяснить различие в коэффициентах пропорциональности для доходов (убытков) компаний на разных рынках?
-
Как изменится запись функций выигрыша, если каждая компания получает доход на рынке при долевом преобладании своей продукции и не получает ничего в противном случае?
-
Составьте математическую модель игры для двух компаний и трех рынков при тех же условиях получения доходов и убытков.
-
Составьте сходную математическую модель игры для трех компаний и двух рынков.
-
Приведите пример операции, которая формализуется так же, как рассматриваемая игра.
Начало раздела 1
Следующий раздел 2
Содержание пособия
Теперь проверьте свои знания, полученные при изучении этого раздела курса, с помощью нескольких заданий в тестовой форме.
По всем вопросам относительно данного учебного пособия можно обращаться к автору, - Ащепкову Леониду Тимофеевичу