2. ЗАДАЧА УПРАВЛЕНИЯ ЗАПАСАМИ

  Объектом нашего внимания будет задача управления запасами, которая в принятых в примере 1.1 обозначениях имеет вид

З(х)  =  с₁ N / x + 0.5 с₂ Т x  →  min,  х > 0.                    (2.1)

Отвлекаясь пока от экономического и физического смысла величин, будем рассматривать  с₁ , с₂ , N,  Т   как положительные параметры (исходные данные задачи, которые могут принимать любые положительные действительные значения и не меняются в процессе решения); х – как неизвестную (переменную величину) с положительными действительными значениями, З(х) – как заданную формулой (2.1) функцию с областью определения 0 < х < ∞.

        2.1.  Решение задачи.  Целевая функция (2.1) естественно задает отношение предпочтения. Из двух положительных чисел   х₁,  х₂  первое не хуже (предпочтительней) второго, если  З(х₁)  ≤  З(х₂). Оптимальным (наилучшим) решением считаем число  х*  > 0,  которое не хуже любого другого числа  х > 0.

      Существование и единственность решения  х*  легко устанавливается геометрически. Как видно из формулы (2.1), целевая функция   З(х)  есть сумма функций

З₁(х) = с₁ N / x ,          З₂(х) = 0.5 с₂ Т x.

График первой из них гипербола, график второй – прямая с положительным угловым коэффициентом, проходящая через начало координат. При каждом   х  ордината функции  З(х)  получается сложением соответствующих ординат гиперболы и прямой (рис. 2.1).

     Из рис. 2.1 видно, что функция  З(х)  имеет единственную точку минимума. Согласно необходимому условию экстремума, в точке минимума х = х*  производная    З′(х)  должна обращаться в нуль:

 З′(х)  = -с₁N / х²   + 0.5 с₂ Т = 0.                                 (2.2)

Решив уравнение относительно  х  и отбросив посторонний отрицательный корень, получим

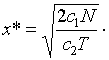                                                   (2.3)

Это и есть оптимальное решение – искомое количество товара в порции (т), доставляемой на склад.

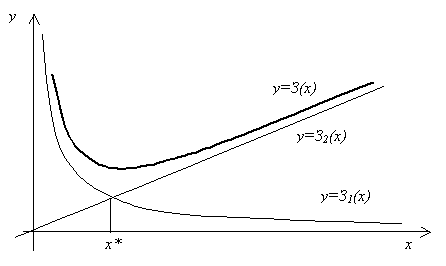
                                      Рис. 2.1. График функции затрат

         2.2.  Анализ решения. Согласно принятому допущению параметры задачи могут принимать любые положительные действительные значения. Вполне возможно, что при некотором их сочетании формула (2.3) даст иррациональное число, например,  х* = π.  С точки зрения здравого смысла рекомендация завезти на склад   π  тонн товара выглядит несколько абсурдно. Однако это не означает непригодность решения (2.3). Это означает лишь, что иррациональное число  х*  следует заменить подходящим рациональным приближением   у*.  Конечно, соответствующие затраты  З(у*) будут отличаться от минимальных  З(х*), но в силу непрерывности функции затрат отличие будет тем меньше, чем ближе  у*  к   х*. В нашем примере число π = 3.141593... имеет бесконечную непериодическую дробную часть, поэтому с приемлемой точностью можно взять одно из приближений:

 х* ≈ у* = 3.1 т;             х* ≈ у* = 3.14 т;           х* ≈ у* = 3.141 т; … .

        Другое допущение (неизвестная  х  принимает любые положительные действительные значения) было использовано при составлении и решении уравнения (2.2). Если количество товара выражается в неделимых единицах, (например, речь идет о телевизорах, холодильниках, комплектующих деталях и т. д.), то это допущение не отвечает действительности и должно быть заменено условием целочисленности переменной  х. Приняв условие целочисленности, мы получим уже другую задачу. Для нее уравнение (2.2) не имеет смысла,  значит, не имеет смысла и решение (2.3). В этом случае надо использовать другие методы нахождения решения, которые явно или не явно учитывают условие целочисленности неизвестной. С некоторыми из них мы познакомимся позже в курсах линейного и нелинейного программирования и исследования операций.

        2.3. Чувствительность решения к исходным данным. Остановимся на важном в практическом отношении вопросе о зависимости решения (2.3) от исходных данных. В общем случае параметры  с₁ , с₂ , N,  Т  определяются экономическими расчетами или оцениваются экспертно и известны приближенно с некоторыми погрешностями. Кроме того, в силу разных причин их значения могут меняться со временем. Возникает необходимость оценить влияние малых погрешностей (или малых изменений исходных данных) на решение (2.3).

      Покажем, как можно сделать такую оценку по одному из параметров при фиксированных значениях других. Пусть для определенности нас интересует влияние на решение (2.3) потребности  N  в товаре при неизменных стоимостях  с₁, с₂  его доставки и хранения и длительности  Т  планового периода. Считая  N  > 0, представим формулу (2.3) в виде

 .

Придадим аргументу  N  достаточно малое по абсолютной величине приращение  Δ N   и составим приращение функции

 Δх*= х*(N + ΔN) - х*(N)= .

Отнесем приращение  Δх*   к  ΔN, т. е. выясним, какое приращение затрат  приходится на единицу потребности в товаре,

.

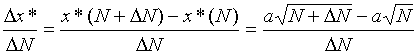Устремим теперь  ΔN  к нулю произвольным способом. По определению производной в пределе получим

.

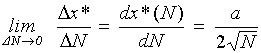     Производную

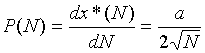                                            (2.4)

будем считать показателем чувствительности решения  х*(N + ΔN) к малым приращениям  ΔN.  Действительно, для малых  ΔN  из трех последних равенств имеем

.

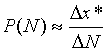Следовательно,

Δх* ≈ Р(N) ΔN.                                           (2.5)

Формулой (2.5) удобно пользоваться для приближенного вычисления приращения решения при малом приращении  ΔN.

          2.4. Пример. Вычислим оптимальную порцию товара при   a = 1 т^1/2 и  N = 100 т. Имеем

х*(100) =  = 10 т.

Выясним, как изменится порция товара, если потребность увеличиться на  2 т.   С этой целью по формуле (2.4) подсчитаем предварительно показатель чувствительности

.

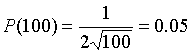Принимая  ΔN = 2  и используя формулу (2.5), находим искомое приращение решения

Δх* ≈ Р(100) x 2 = 0.05 x 2 = 0.1 т.

В результате получим

х*(102)= х*(100) + Δх* ≈ = 10 + 0.1 = 10.1 т.

       Чувствительность решения к другим исходным данным можно определить таким же способом. Например, если нас интересует чувствительность решения к стоимости   с₂  (хранения товара), то надо представить формулу (2.3) в виде

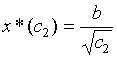
и повторить приведенные выше рассуждения для функции   х*(с₂).

       2.5. Относительная чувствительность. При анализе решения на чувствительность полезно знать, на сколько процентов изменится оптимальное решение по отношению к своему номинальному (первоначальному) значению, если потребность в товаре изменится на заданное число процентов.

      Ответ на вопрос практически уже содержится в формуле (2.5). Разделим приближенное равенство (2.5) на . Учитывая  вид (2.4) показателя чувствительности и выполняя очевидные преобразования, получим

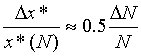
Отсюда видно, что при изменении потребности в товаре на  1%  (ΔN =0.01 N) оптимальная порция товара изменится на  0.5%  по отношению к  х*(N).  

Вопросы и упражнения

1.  Как изменится решение задачи, если в ее условия ввести дополнительное ограничение  х ≤ а  на количество товара в порции?

2.  Будет ли меняться решение задачи при пропорциональном изменении стоимости доставки и хранения товара?

3.  Как влияет на решение увеличение длительности планового периода, увеличение спроса на товар?

4.  Допустим, в качестве товара выступают комплектующие детали, измеряемые в штуках. Как отразится это на условиях задачи?

5.  Можно ли утверждать, что формула (2.3) по-прежнему будет давать решение задачи?

6.  Будет ли решением задачи целое число, полученное округлением числа (2.3) с недостатком или избытком?

7.  Что следует считать показателем чувствительности в данном случае?

8.  Исследуйте относительную чувствительность решения (2.3) к длительности планового периода.

Начало  раздела 2
Предыдущий раздел 1
Следующий раздел 3
Содержание пособия

По всем вопросам относительно данного учебного пособия можно обращаться к автору, - Ащепкову Леониду Тимофеевичу