3. ЗАДАЧА «О ДВУХ КАРТОШКАХ»

Рассмотрим задачу «о двух картошках» из примера 1.2. Напомним, что в ней требуется найти такие значения неизвестных  х₁, х₂, которые обеспечивают максимум функции

  П (х₁, х₂) = 5х₁ + 6х₂

   при условиях 

0.2х₁ + 0.3х₂ ≤ 1.8,

 0.2х₁ + 0.1х₂ ≤ 1.2,

 0.3х₁ + 0.3х₂ ≤ 2.4,

 х₁ ≥ 0, х₂ ≥  0.

Мы будем предполагать, что неизвестные могут принимать любые неотрицательные действительные значения, и все линейные функции в условиях задачи естественным образом определены во всей области изменения неизвестных.

          3.1. Упрощение модели. Чтобы избавиться от дробных коэффициентов, умножим первые два предыдущих неравенства на 10, а третье неравенство - на 10/3. При этом смысл и множество решений каждого неравенства не изменится. В результате получим эквивалентную задачу

 П (х₁, х₂)= 5х₁ + 6х₂ → mах,                                         (А)

 2х₁ + 3х₂ ≤ 18,                                                    (Б)

 2х₁ + х₂ ≤ 12,                                                    (В)

х₁ + х₂ ≤ 8,                                                      (Г)

 х₁ ≥ 0,                                                         (Д)

     х₂ ≥ 0.                                                         (Е)

           Эквивалентность задач (А) – (Е) и (1.6) – (1.10) означает, что они имеют одно и то же множество решений.

          3.2. Оптимальный план. Следуя традиции, точку х = (х₁, х₂) с координатами  х₁, х₂, удовлетворяющую условиям (Б) – (Е) задачи, назовем планом. На координатной плоскости переменных  х₁, х₂  совокупность всех планов образует некоторое множество. Мы будем называть его множеством планов и обозначать  D.

         Целевое условие (А) естественно задает отношение предпочтения между двумя планами. План х = (х₁, х₂), очевидно, не хуже плана у = (у₁, у₂), если П (х₁, х₂) ≥ П (у₁, у₂). План х* = (х₁*, х₂*), который не хуже любого другого плана из множества D, назовем оптимальным.

         Из условий задачи непосредственно не вытекает существование планов и, тем более, оптимальных планов. Покажем, как с помощью простых геометрических построений можно выяснить строение множества планов и найти оптимальный план.

        Начнем с множества планов. Каждое из условий (Б) – (Е) задачи представляет собой линейное неравенство относительно неизвестных  х₁, х₂. Рассмотрим для определенности неравенство

2х₁ + х₂ ≤ 12                                              (3.1)

и соответствующее ему равенство

2х₁ + х₂ = 12.                                             (3.2)

Соотношение (3.2) будем считать уравнением прямой на координатной плоскости. При одной и той же произвольной абсциссе  х₁ ордината  х₂ точки, удовлетворяющей неравенству (3.1), не превосходит ординаты точки на прямой (3.2). Следовательно, совокупность таких точек (решений неравенства (3.1)) образует замкнутую полуплоскость, ограниченную сверху прямой (3.2). На рис. 3.1 прямая (3.2) помечена символом (В).

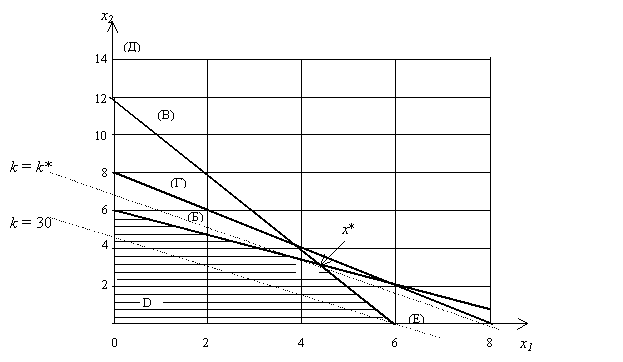
        Рис. 3.1. Множество планов и линии уровня целевой функции в задаче о «двух картошках»

        Такими же рассуждениями строятся решения остальных линейных неравенств (Б), (Г), (Д), (Е). Геометрически они изображаются замкнутыми полуплоскостями, ограниченными  прямыми (Б), (Г), (Д), (Е) (рис.3.1). Общая часть полуплоскостей (четырехугольник D) состоит из точек х = (х₁, х₂), которые отвечают всем условиям (Б) – (Е) задачи. Значит, четырехугольник D и есть множество планов.

         Линию на плоскости переменных  х₁, х₂, в точках которой целевая функция имеет одно и то же постоянное значение, назовем линией уровня целевой функции. Если постоянное значение функции обозначить через  k, то уравнение линии уровня запишется в  виде

П (х₁, х₂) = 5х₁ + 6х₂ = k.                                   (3.3)

Придавая  k  разные числовые значения, получим семейство параллельных прямых. Две из них, отвечающие  k = 30  и  k = k*, приведены на рис. 3.1. Первая прямая пересекает множество планов. Вторая прямая имеет с множеством планов единственную общую точку  х*. При  k > k*  прямые (3.3) не будут иметь с множеством планов общих точек.

          На экономическом языке это означает существование бесчисленного множества планов закупки картофеля у поставщиков, которые приносят одну и ту же относительную прибыль 30 ден. ед; есть только один план  х*  закупки картофеля, который дает  k*  ден. ед. относительной прибыли, и относительная прибыль более  k* ден. ед. невозможна.

         Следовательно, наибольшее значение целевой функции на множестве планов равно  k*  и план  х*  оптимален. Как видно из рис 3.1, оптимальный план лежит на пересечении прямых (Б) и (В). Решая совместно уравнения этих прямых

 2х₁ + 3х₂ = 18,                                         (3.4)

 2х₁ + х₂ = 12,                                          (3.5)

находим его координаты

х₁* = 4.5 т,         х₂* = 3 т.

Максимальная относительная прибыль составляет

k* = П (4.5, 3) = 5 x 4.5  +  6 x 3 = 40.5 ден. ед.

Это и есть решение задачи.

         3.3. Анализ решения. Непосредственными подсчетами легко убедиться, что на оптимальном плане ограничения (Б), (В) задачи выполняются в форме равенств (активны), а остальные – в форме строгих неравенств (не активны). Если из условий задачи убрать неактивные ограничения и оставить только активные, то решение задачи не изменится. Очевидно, неактивные ограничения останутся неактивными при небольших изменениях входящих в них коэффициентов. Более того, если и в активных ограничениях немного изменить все коэффициенты, то они по-прежнему будут активными и определят новый оптимальный план. Другими словами, оптимальный план обладает свойством структурной устойчивости по отношению к малым «шевелениям» активных и неактивных ограничений.

          На экономическом языке малое шевеление ограничений (Б), (В), (Г) означает малые количественные изменения в выходе готовой продукции из одной т картофеля каждого поставщика и малые изменения в спросе на готовую продукцию. Структурная устойчивость позволяет выяснить количественную зависимость оптимального плана от этих факторов производства.

          Действительно, запишем уравнения (3.4), (3.5) с измененными коэффициентами в виде

(2 + Δа₁₁)х₁ + (3 + Δа₁₂)х₂ = (18 + Δb₁),                          (3.6)

(2 + Δа₂₁)х₁ + (1 + Δа₂₂)х₂ = (12 + Δb₂),                           (3.7)

где  приращения   Δа₁₁, Δа₁₂,…, Δb₂ коэффициентов достаточно малы по абсолютной величине. Тогда определитель

Δ = - 4 + Δа₁₁ - 2 Δа₁₂- 3 Δа₂₁ + 2 Δа₂₂  +…

системы уравнений (3.6), (3.7) отличен от нуля, и ее решение можно записать по формулам Крамера

х₁*= Δ₁/Δ,   х₂*= Δ₂/Δ;                                             (3.8)

Δ₁= - 18 + Δа₁₁ - 12Δа₁₂ + 18Δа₂₂+ Δb₁ - 3Δb₂ +… ;                  (3.9)

Δ₂= - 12 + 12Δа₁₁– 18 Δа₂₁– 2 Δb₁+ 2 Δb₂ +…  .                 (3.10)

Многоточием обозначены члены более высокого порядка малости, чем наибольшая из абсолютных величин |Δа₁₁|, | Δа₁₂|, … , |Δb₂|.

          Чтобы подсчитать отношения  Δ₁/Δ  и  Δ₂/Δ, воспользуемся известной формулой

(1 – q)^-1 = 1 + q + q² +…

для суммы членов геометрической прогрессии со знаменателем q (|q| < 1).

Полагая в формуле  q = Δа₁₁ - 2Δа₁₂ - 3Δа₂₁ + 2Δа₂₂ + …,  получим

Δ^-1 = (- 4 + q)^-1 = (-1/4) (1 – q/ 4)^-1 = 

=- 1/4(1 – q /4 + ...) = - 1/4 + q/16 + … =

= - 1/4 + (Δа₁₁ - 2Δ а₁₂ – 3Δа₂₁   + 2Δ а₂₂)/ 16 + … .      (3.11)

Подставим выражения (3.9) – (3.11) в (3.8). Выполнив необходимые преобразования, найдем искомую зависимость оптимального плана от малых приращений коэффициентов

х₁* = 9/ 2 + (-11Δа₁₁ + 36Δа₁₂ + 27Δа₁₂ - 54Δ а₂₂)/ 8 +

    + (-Δb₁ + 3Δb₂)/ 4  + …,

х₂* = 3 + (- 15Δ а₁₁ + 6Δа₁₂ + 27Δа₂₁ - 6Δ а₂₂)/ 4+

 + (Δ b₁ -Δ b₂)/ 2  + … .                                    (3.12)

            Если приращения коэффициентов нулевые, то получим уже известное нам точное решение задачи. Множители при приращениях коэффициентов в правых частях формул (3.12) есть показатели чувствительности решения к соответствующим факторам производства. Сравнивая показатели чувствительности, мы видим, что при единичных приращениях всех коэффициентов на первую координату оптимального плана в наибольшей степени влияет Δа₂₂   и в наименьшей степени –  Δb₁. На вторую координату – соответственно  Δа₂₁   и  Δb₁, Δb₂. Таким образом, из всех факторов производства наибольшее влияние на оптимальный план оказывают выходы кубиков из одной тонны картофеля каждого поставщика и в наименьшей степени – спрос на готовую продукцию.

Вопросы и упражнения

1. Как надо изменить свободный член ограничения (Г), чтобы оно стало активным на оптимальном плане?

2. На сколько надо уменьшить свободный член ограничения (Г), чтобы точка с координатами  х_!* = 4.5, х₂* = 3  перестала быть планом задачи? Какие вершины множества планов станут при этом оптимальными планами? Обоснуйте выводы расчетами, объясните экономически.

3. Что происходит с решением задачи при малых «шевелениях» одного ограничения (Б), одного ограничения (В)?

4. Выясните, при каких относительных прибылях план  х* = (4.5, 3)   оптимален?

5. Найдите, при каких относительных прибылях имеет место не единственность решения задачи? Опишите соответствующие множества оптимальных планов.

6. С использованием формул (3.12) запишите формулы относительной чувствительности координат оптимального плана к малым приращениям исходных данных. Если исходные данные меняются не более, чем на один процент по отношению к номинальным значениям, то какие из исходных данных по отдельности вызывают наибольшее и наименьшее изменение координат оптимального плана?

7. Приведите примеры операций, которые формализуются в виде задач линейного программирования.

8. Придумайте и запишите примеры задач линейного программирования с двумя неизвестными, в которых

        -множество планов пусто; состоит из одного плана; не ограничено;

        -решение единственное; не единственное;

        -решение отсутствует из-за неограниченности целевой функции на множестве планов.

Начало раздела 3
Предыдущий раздел 2
Следующий раздел 4
Содержание пособия