4. ПРОИЗВОДСТВЕННАЯ ЗАДАЧА «МЕСТА И ВРЕМЕНИ»
Обратимся к
примеру 1.3, в котором была описана производственная задача «места и времени». В математической формулировке она состоит в нахождении таких значений неизвестных
х1 и х2, которые доставляют минимум функции
С (х1,
х2) = х12/с1 + х22/с2 → min (4.1)при ограничениях
х 1 + х2 = а, х1 ≥ 0, х2 ≥ 0. (4.2)
4.1. Предположения. Будем предполагать, что в задаче (4.1), (4.2) положительные параметры а, с1 и с2 заданы, неизвестные х1, х2 принимают любые неотрицательные действительные значения и функция С (х1, х2) определена при х1 ≥ 0, х2 ≥ 0.
4.2. Преобразование задачи. Как и ранее, точки х = (х1, х2) плоскости переменных х1, х2, удовлетворяющие условиям (4.2) задачи, назовем планами. Множество планов обозначим D. Геометрически множество D представляет собой отрезок прямой х1 + х2 = а, расположенный в первой координатной четверти (рис 4.1).
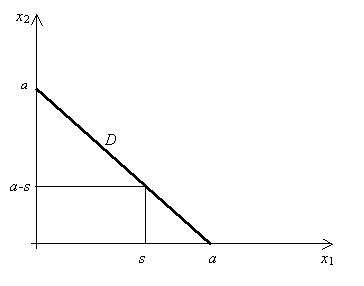
Рис. 4.1. Множество D планов в производственной задаче «места и времени»
Функция стоимости С(х) ≡ С(х1, х2) задает на множестве планов отношение предпочтения: чем меньше «стоимость» плана, тем он предпочтительней. Решением задачи естественно считать оптимальный (самый предпочтительный) план х* = (х1*, х2*) со свойством С(х*) ≤ С(х) по отношению к любому другому плану х = (х1, х2).
Нахождение оптимального плана заметно упрощается, если условия (4.2) задачи предварительно преобразовать. Параметризуем точки множества D, полагая
х 1 = s , х2 = а - s , 0 ≤ s ≤ а, (4.3)
где s – новая переменная. При непрерывном изменении s от 0 до а точка с координатами (4.3) пробегает все множество D. Подставим выражения (4.3) в формулу (4.1). Обозначив
С (s, а - s) ≡ С1(s), (4.4)
получим редуцированную (преобразованную) задачу
С 1 (s) = s2/ с 1 + ( а – s)2/ с 2 → min , 0 ≤ s ≤ а . (4.5)
Редуцированная задача (4.5) равносильна исходной (4.1), поскольку между планами множества D и точками отрезка [0, а] существует взаимно однозначное соответствие (4.3), и функция С1(s) на основании равенства (4.4) совпадает с целевой функцией С(х1, х2). Если точка минимума s* в редуцированной задаче найдена, то по формулам (4.3) находится решение и исходной задачи :
х 1 * = s*, х2* = а – s*. (4.6)
4.3. Оптимальный план. В силу задания (4.5) целевая функция С1(s) есть квадратный трехчлен. Возводя разность а – s в квадрат и приводя подобные члены, получим
С 1 (s) = (с1-1 + с2-1) s2 + 2ас2-1 s + а2с2-1.
Выделим в правой части полный квадрат. После очевидных преобразований имеем
С 1 (s) = (с1-1 + с2-1) [ s - ас1(с1 + с2)-1]2 + а2 (с1 + с2)-1. (4.7)
На отрезке 0 ≤ s ≤ а функция (4.7) имеет единственную точку минимума
s* = ас1(с1 + с2)-1, (4.8)
с соответствующим значением функции
С 1 (s*) = а2(с1 + с2)-1. (4.9)
Формулы (4.8), (4.9) дают решение редуцированной задачи. Используя связи (4.6), находим интересующее нас решение первоначальной задачи
х 1 * = ас1(с1 + с2)-1, х2* = ас2(с1+ с2)-1, (4.10)
С (х1*, х2*) = а2(с1 + с2)-1. (4.11)
4.4. Анализ решения. Оптимальный план выражается через исходные данные а, с1 и с2 и интересен в экономическом отношении. Если с1 > с2, то производство единицы продукции на первом заводе дешевле, чем на втором. Поэтому, выгоднее изготовить большую долю заказа на первом заводе и меньшую – на втором. Согласно формулам (4.10) долевое распределение заказа в общем случае должно быть пропорциональным величинам с1 и с2 с одним и тем же коэффициентом пропорциональности а(с1 + с2)-1.
Анализ оптимального плана на чувствительность к исходным данным проводится по стандартной схеме. Мы не будем на нем останавливаться, предоставив читателю возможность попробовать свои силы самостоятельно. Важнее обсудить пути обобщения результатов.
Предположение о характере изменения неизвестных х1, х2 было использовано в рассуждениях дважды: при конкретизации области определения целевой функции (4.1) и в формулах (4.10). Вместе с тем способ получения формул (4.10) непосредственно на это предположение не опирается и в принципе годится для другого (целочисленного) варианта задачи.
Пусть, например, рассматривается задача о распределении между двумя заводами заказа на изготовление а неделимых единиц продукции. Тогда неизвестные х1, х2 по смыслу неотрицательные и целые. Если воспользоваться параметризацией множества планов с помощью целочисленной переменной s = 0,1, ..., а и подсчитать целевую функцию (4.4), то внешне она совпадет с функцией (4.7), но будет определена на конечном множестве S = { 0,1, ..., а } изменения аргумента s.
Точка s* минимума С1(s) на S получается округлением числа s0 = ас1(с1 + с2)-1 до ближайшего целого. Действительно, поскольку 0 < s0 < а, то 0 ≤ s* ≤ а. Кроме того, из неравенства
ï s* - s 0 ï ≤ ï s - s 0 ï , s = 0,1,..., а
в силу (4.7) вытекает С1(s*) ≤ С1(s) для точек s из S, что и дает требуемое.
Если обозначить через [s0] целую часть числа s0, то в соответствии со сказанным
s* = [s0] при [s0] ≤ s 0 ≤ [s0] + 0.5;
s* = [s0] + 1 при [s0] + 0.5 ≤ s 0 ≤ [s0] + 1.
Координаты искомого оптимального плана для целочисленной задачи найдутся по формулам (4.6).
Вопросы и упражнения
Найдите минимум функции (4.5), приравняв нулю ее первую производную. Сравните полученный вывод с результатом (4.10), (4.11). Можно ли утверждать, что применение необходимого условия экстремума в данном случае корректно и гарантированно даст искомую точку минимума? Почему?
Исследуйте решение (4.10), (4.11) на чувствительность и относительную чувствительность к исходным данным.
Сформулируйте задачу при дополнительных ограничениях на производственные мощности заводов-изготовителей продукции. Как должны быть согласованы эти ограничения с остальными ограничениями для разрешимости задачи? Поясните геометрическими построениями.
Попробуйте решить задачу при дополнительных ограничениях на производственные мощности заводов-изготовителей продукции, используя аналог преобразования (4.3). Всегда ли для решения задачи применимы необходимые условия экстремума? Почему?
Начало раздела 4
Предыдущий раздел 3
Следующий раздел 5
Содержание пособия
По всем вопросам относительно данного учебного пособия можно обращаться к автору, Ащепкову Леониду Тимофеевичу