5. ИГРА «ПРЕСЛЕДОВАНИЕ ШЕРЛОКА ХОЛМСА»

5.1. Матрица выигрышей. Игра, которую мы подробно рассмотрели в примере 1.4, задана таблицей 1.2. Чтобы определить наилучшие действия игроков, удобно по таблице 1.2 сформировать матрицу выигрышей

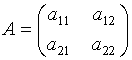
с элементами

а₁₁ = - 100,        а₁₂ = 50,       а₂₁ = 100,        а₂₂ = - 100.          (5.1)

          В терминах матрицы выигрышей стратегиями игроков служат номера ее строк и столбцов. Если первый игрок выбрал строку  i  и второй игрок – столбец  j, то в игре складывается ситуация  (i, j). В этой ситуации первый игрок получает в качестве выигрыша элемент  а_ij, стоящий на пересечении строки i  и столбца  j. Выигрыш второго игрока принимается равным  - а_ij . Если элемент  а_ij  положительный, то выигрыш -а_ij  второго игрока трактуется как проигрыш. Цель каждого игрока, как и ранее, состоит в максимизации индивидуального выигрыша путем выбора одной из его стратегий.

         5.2. Оптимальные стратегии. В матричной игре каждый из игроков выбирает свои стратегии, не имея сведений о действиях другого игрока. Выясним, на какие наилучшие гарантированные выигрыши они могут рассчитывать. Первый игрок, выбрав некоторую стратегию  i, может получить в качестве выигрыша один из двух элементов  а_i1, а_i2  матрицы  А  в зависимости от того, какую стратегию применит второй игрок. В худшем случае он должен рассчитывать на минимальный выигрыш, т. е. на

  .

 В то же время при удачном выборе стратегии  i = i*  первый игрок может получить максимальный выигрыш из минимальных:

                               (5.2)

          Второй игрок рассуждает сходным образом. При выборе стратегии  j  его максимальный проигрыш из двух возможных  а_{1 j}, а_{2 j}  равен

  . 

Если выбор стратегии  j = j*  оказался удачным, то он может рассчитывать на минимальный проигрыш из максимальных:

.                                     (5.3)

        Формулы (5.2), (5.3) определяют наилучшие гарантированные выигрыши игроков. Если они совпадают, то их общее значение можно считать приемлемым для игроков компромиссом, а соответствующие стратегии  i*,  j*  - оптимальными стратегиями.

        Непосредственные вычисления по формулам (5.2), (5.3) с использованием (5.1) дают

Здесь наилучшие гарантированные выигрыши не равны и оптимальных стратегий не существует.

        Причина отсутствия оптимальных стратегий кроется, очевидно, в их определении. Попробуем  изменить определение оптимальных стратегий, не упуская из вида игрового смысла задачи и целей игроков.

         5.3. Смешанное расширение игры. Допустим, игроки мысленно разыгрывают игру  n  раз и решают ориентироваться на те стратегии, которые приносят наилучшие средние выигрыши. Более точно, предположим, что за  n  партий первый игрок выбрал стратегии  i = 1,  i = 2  соответственно  m₁  и  m₂  раз, и второй игрок стратегии  j = 1,  j = 2 -  соответственно  n₁  и  n₂  раз. По предположению

m₁ + m₂ = n,          n₁ + n₂  = n.                                      (5.4)

        Подсчитаем средний выигрыш первого игрока  за   n  партий. Если первый игрок во всех партиях использует стратегию  i = 1, то его общий выигрыш составит  а₁₁n₁ + а₁₂n₂. При этом средний выигрыш за одну партию равен

(а₁₁n₁  +  а₁₂n₂)/n

и за  m₁  партий

m₁(а₁₁n₁ + а₁₂ n₂)/n.                                   (5.5)

Точно так же выигрыш первого игрока за   m₂  партий составит

m₂(а₂₁n₁ + а₂₂n₂)/n.                                    (5.6)

Суммируя выигрыши (5.5), (5.6), получим общий выигрыш

m₁(а₁₁n₁ + а₁₂n₂)/n  +  m₂(а₂₁n₁ + а₂₂n₂)/n

и искомый средний выигрыш

Н = m₁(а₁₁n₁ + а₁₂n₂)/n² + m₂(а₂₁n₁ + а₂₂n₂)/n²             (5.7)

первого игрока за  n  партий.

Обозначим через

х₁ = m₁/ n,   х₂ = m₂/ n,   у₁ = n₁/ n,   у₂ = n₂/ n ,            (5.8)

частоты выбора «чистых» стратегий  i = 1,  i = 2,  j = 1,  j = 2  соответственно. Тогда формула (5.7) запишется в виде

Н(х₁, х₂, у₁, у₂) = а₁₁х₁у₁  +  а₁₂х₁у₂  +  а₂₁х₂у₁  +  а₂₂х₂у₂.             (5.9)

Непосредственно из равенств (5.4) и определения (5.8) следует

х₁ + х₂ = 1,       х₁ ≥ 0,        х₂ ≥ 0,                                   (5.10)

у₁ + у₂ = 1,       у₁ ≥ 0,         у₂ ≥ 0.                                  (5.11)

         Точки  х = (х₁, х₂)  и  у = (у₁, у₂), отвечающие условиями (5.10) и (5.11), назовем смешанными стратегиями первого и второго игрока. Множества смешанных стратегий обозначим  Х  и  Y.

         Игру  Г, заданную тройкой  Х, Y, Н, называют смешанным расширением матричной игры. Легко видеть, что, смешанное расширение однозначно строится по матрице выигрышей  А.

         Координатами (5.8) смешанных стратегий являются рациональные числа. Чтобы обеспечить разрешимость игры  Г, определим эти координаты на более широком множестве всех действительных чисел, удовлетворяющих условиям (5.10), (5.11). Тогда множествами смешанных стратегий  Х, Y  станут отрезки прямых на координатных плоскостях переменных  х₁, х₂  и  у₁, у₂, и функция

Н(х, у) ≡ Н(х₁, х₂, у₁, у₂)

естественным образом продолжится все действительные точки отрезков. Смешанные стратегии и значения функции  Н(х, у)  по-прежнему будем трактовать как «частоты» выбора чистых стратегий и как «средние» выигрыши.

        Смешанные стратегии  х*, у*  назовем оптимальными в игре  Г, если для любых стратегий  х, у  выполнены неравенства

 Н (х, у*) ≤ Н (х*, у*) ≤ Н (х*, у).                         (5.12)

Левое неравенство (5.12) показывает, что стратегия  х = х*  в ситуациях  (х, у*) обеспечивает первому игроку наибольший «средний» выигрыш  Н(х*, у*). Правое неравенство означает, что в ситуациях  (х*, у)  стратегия  у = у*  гарантирует второму игроку минимальный проигрыш  Н(х*, у*). В этом смысле стратегии  х*, у*  являются для игроков наилучшими.

         5.4. Решение игры в смешанных стратегиях. Из определения (5.12) непосредственно не следует существование оптимальных смешанных стратегий. Для их нахождения параметризуем точки множеств  Х, Y, полагая на основании (5.10), (5.11)

 х = (х₁, х₂) = (р, 1 - р),   0 ≤ р ≤ 1;

у = (у₁, у₂) = (q, 1 - q),   0 ≤ q ≤ 1.                             (5.13)

          Подставим  элементы (5.1) матрицы выигрышей и стратегии (5.13) в формулу (5.9). После очевидных преобразований получим

Н (р, 1- р, q, 1- q) ≡ Н₁(р, q) = -350 рq + 150 р + 200 q – 100.                (5.14)

Преобразуем теперь функцию (5.14) к виду

Н₁(р, q) = -350 (р – а)(q – b) + с,                               (5.15)

где  а, b, с – некоторые постоянные. Раскрывая скобки, имеем

Н₁(р, q)) = -350 рq + 350 bр + 350 аq – 350 аb + с.             (5.16)

Функции (5.14) и (5.16) будут тождественно совпадать при любых 0 ≤ р ≤ 1, 0 ≤ q ≤ 1  в том и только в том случае, если выполнены равенства

350 а = 200,       350 b = 150,      – 350 аb + с = -100.

Отсюда последовательно находим  а = 4/7,  b = 3/7,  с = -100/7. В результате формула (5.15) примет вид

Н₁(р, q) = –350 (р – 4/7) (q – 3/7) – 100/7.                   (5.17)

         В силу однозначного соответствия (5.13) между смешанными стратегиями  х, у  и числами  р, q  можно считать, что сами числа  р, q  из отрезков  0 ≤ р ≤ 1,  0 ≤ q ≤ 1  являются «стратегиями» игроков и соответствующая им функция средних выигрышей задана формулой (5.17). В такой трактовке первому игроку целесообразно выбрать число  р* = 4/7, которое обеспечит ему средний выигрыш  -100/7  при любой «стратегии»  q  второго игрока. Из тех же соображений число  q* = 3/7  предпочтительнее для второго игрока, поскольку оно гарантирует ему средний проигрыш  -100/7  при любой «стратегии»  р  первого игрока. Таким образом, есть основания считать стратегии

х* = (р*, 1 – р*) = (4/7, 3/7),  у* = (q*, 1 – q*) = (3/7, 4/7)             (5.18)

оптимальными  в игре  Г.  В самом деле, на основании (5.14) и (5.17) можем записать

Н (р, 1- р, q, 1- q) = -350 (р – 4/7) (q – 3/7) – 100/7

или в обозначениях (5.13)

Н (х₁, х₂, у₁, у₂) = -350 (х₁ – 4/7) (у₁ – 3/7) – 100/7.

Отсюда с учетом (5.18) находим

Н (х, у*) = -100/7,      Н(х*, у*) = -100/7,      Н(х*, у) = -100/7

для любых стратегий  х, у . Следовательно, стратегии  х*, у*  удовлетворяют критерию оптимальности (5.12).

          5.5. Интерпретация и анализ решения. В теории вероятностей частоты  х₁, х₂, у₁, у₂  трактуются как вероятности выбора игроками своих чистых стратегий, а функцию (5.9) средних выигрышей – как математическое ожидание выигрыша. Решение (5.18) показывает, что первый игрок (Шерлок Холмс) должен с вероятностью  4/7  выбрать чистую стратегию  i = 1  (сойти с поезда в Кентербери) и с вероятностью  3/7  выбрать чистую стратегию  i = 2  (сойти с поезда в Дувре). Тогда математическое ожидание его выигрыша составит  -100/7. Второму игроку (профессору Мориарти) предписывается выбирать чистые стратегии  j = 1,  j = 2  (сойти с поезда в Кентербери и Дувре) с вероятностями  3/7  и  4/7  соответственно. В этом случае математическое ожидание его проигрыша тоже будет -100/7. Если игроки будут следовать указанным рекомендациям, то Шерлок Холмс в «среднем» проиграет примерно  14%  своей «жизни» (его выигрыш –100/7 отрицателен), а профессор Мориарти в «среднем» такую же часть его жизни выиграет (его проигрыш –100/7 отрицателен).

          Читатель, внимательно следивший за ходом рассуждений, возможно, заметил некоторую «осторожность» оптимальных рекомендаций. Вместо однозначных указаний игрокам по выбору чистых стратегий регламентируются лишь вероятности их применения. Более того, читатель вполне резонно может возразить, что при однократном розыгрыше игры (который подразумевается) польза от таких рекомендаций невелика. Игроки должны будут указать свои чистые стратегии только один раз, и их выигрыши в сложившейся ситуации могут значительно отличаться от расчетных «средних» выигрышей.

          По большому счету читатель прав, и в ответ можно привести лишь два «утешительных» довода. Во-первых, лучше иметь какие-то оценки действий игроков, чем не иметь ничего («синица в руках лучше журавля в небе»). И, во-вторых, существует большое количество матричных игр, которые разыгрываются многократно (например, «орлянка»). В них применение смешанных стратегий вполне оправдано. Более того, средствами теории вероятностей можно показать, что если игроки выбирают свои чистые стратегии с предписанными оптимальными вероятностями, то по мере роста числа сыгранных партий средние арифметические их фактических выигрышей будут приближаться к расчетным наилучшим математическим ожиданиям выигрышей. В этом смысле переход к смешанному расширению матричной игры вполне оправдан.

          Отметим, что ключевым моментом в решении задачи было преобразование функции (5.14) средних выигрышей к виду (5.17). Вообще говоря, оно не связано с конкретными числовыми значениями (5.1) матрицы выигрышей и в принципе может быть выполнено для любой матрицы   А  указанного типа. Таким образом, мы не только смогли решить конкретный пример, но и получили в распоряжение определенный способ решения матричных игр с матрицами выигрыша размера 2x2.

           5.6. Анализ решения на чувствительность к исходным данным. При построении модели матричной игры в примере 1.4 выигрыши Шерлока Холмса в разных ситуациях были определены равенствами (5.1).По поводу численных значений выигрышей мнения студентов на лекционных занятиях, обычно, разделяются. Выигрыш   а₂₁ = 100  в ситуации, когда Холмс сходит с поезда в Дувре, а Мориарти – в Кентербери, сомнений не вызывает. Как правило, дискуссия разгорается вокруг выигрыша  а₁₂ = 50,  (Холмс и Мориарти сходят с поезда в Кентербери и Дувре соответственно). В связи с этим интересно и полезно выяснить влияние элементов матрицы выигрышей (исходных данных) на решение игры, т. е. на оптимальные смешанные стратегии и математическое ожидание выигрыша. Чтобы не усложнять изложение, ограничимся выяснением влияния элемента  а₁₂ ≡ а, 0 ≤ а ≤ 100,  на решение игры  Г_а  с матрицей выигрышей

.

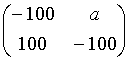          Используя формулы (5.2), (5.3), найдем наилучшие гарантированные выигрыши игроков

При любом значении  а  из отрезка [0, 100] наилучшие гарантированные выигрыши различны, следовательно, игра  Г_а  не имеет решения в чистых стратегиях.

        Обозначим через Н_а(р, q)  функцию средних выигрышей в игре  Г_а. Используя описанный в п. 5.4 прием преобразования функции средних выигрышей, получим

Н_а(р, q) = - (а + 300) рq + (а + 100) р + 200 q – 100 =

=-(а + 300) [p – p(a)] [q – q(a)] + r(a),

где

          Найдем области значений функций  p(a), q(a)  при  0 ≤ а ≤ 100. Имеем

Поскольку области значений функций лежат на отрезке [0,1], решение игры  Г_а  примет вид

х*(а) = (р(а), 1– р(а)),  у*(а) = (q(а), 1– q(а)),  v = r(a).               (5.19)

          Теперь легко оценить уклонение решений (5.18) и (5.19) игр Г_{а = 50}   и  Г_а.  Для первых координат оптимальных стратегий при любых  а,  0≤   а≤ 100,  находим

Аналогично оценивается уклонение по вторым координатам оптимальных стратегий. Максимальное по абсолютной величине уклонение не превосходит числа ε = 2/21. По отношению к числам  p* = 4/7, q* = 3/7  максимальное уклонение составляет

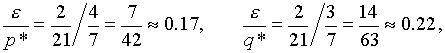
т.е. примерно  17%  и  22%.  Таким образом,  при изменении элемента  а₁₂≡ а матрицы выигрышей от 0 до 100 координаты оптимальных стратегий (5.19) меняются не более, чем на  22% по отношению к координатам стратегий (5.18).    

Вопросы и упражнения

1.  Покажите, что наилучшие гарантированные выигрыши игроков связаны соотношениями

2.  Докажите теорему о минимаксе:  наилучшие гарантированные выигрыши равны, т. е.

,

        тогда и только тогда, когда матрица    А    имеет  седловую  точку

         (i*,  j*) со  свойством

       для любых индексов  i, j = 1,2.

3. Каким характеристическим свойством обладает элемент матрицы выигрышей, соответствующий седловой точке? Можно ли считать, что седловая точка образована оптимальными стратегиями игроков?

4. Докажите «прямоугольное» свойство седловых точек. Если  (i₁, j₁)  и  (i₂, j₂) – седловые точки матрицы выигрышей, то  (i₁, j₂)  и  (i₂, j₁)  тоже будут седловыми точками той же матрицы выигрышей.

5. Какие из приведенных ниже матриц

,     ,     ,    

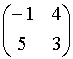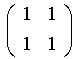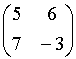
        имеют седловые точки?

6. Попробуйте проделать преобразования п. 5.4 для произвольной матрицы выигрышей размера 2 x 2.

7. Можно ли способ нахождения решений игры, указанный в задании 6, считать доказательством ее разрешимости в смешанных стратегиях?

8. Найдите для матриц из задания 5, не имеющих седловых точек, решения в смешанных стратегиях.

Начало раздела 5
Предыдущий раздел 4
Следующий раздел 6
Содержание пособия

По всем вопросам относительно данного учебного пособия можно обращаться к автору, - Ащепкову Леониду Тимофеевичу