7. ИГРА «БОРЬБА ЗА РЫНКИ»

Напомним, что в рассматриваемой игре (пример 1.6) моделируется конкурентная борьба двух компаний за рынки сбыта своей продукции. Стратегиями компаний служат доли продукции, направляемые на рынки. Преимущество получает компания, сумевшая сосредоточить на рынке большую долю продукции. В формальной математической постановке требуется найти такие значения неизвестных   х  и  у,  которые доставляют максимум функциям доходности

  Н₁( х, у)= k₁ ( х – у)→ max,     Н₂( х, у) = k₂ ( х – у)→ mах               (7.1)

при условиях

0 ≤  х ≤  1,  0 ≤ у ≤1,                                    (7.2)

где  k₁ = k₁₁– k₁₂,  k₂= k₂₂ – k₂₁- заданные коэффициенты. Как и ранее, полагаем, что неизвестные  х  и  у могут принимать любые действительные значения из указанных отрезков.

        7.1. Преобразование задачи. Введем новую неизвестную

s = х – у.                                                    (7.3)

Тогда условия (7.1), (7.2) задачи перепишутся в виде

Н ₍₁₎ ( s)= k₁ s → mах ,     Н₍₂₎ ( s) = k₂ s  → mах ,     -1 ≤ s ≤ 1.            (7.4)

           Решение задачи (7.4) очевидно, если коэффициенты  k₁, k₂  одновременно положительны, отрицательны или равны нулю:

s* = 1   при   k₁ > 0,  k₂ > 0;    s* = -1   при   k₁ < 0,  k₂ < 0;

 -1  ≤   s*  ≤  1   при   k₁ = k₂ = 0.

Из равенства (7.3) и условий (7.2) находим соответствующие  s*  стратегии  х*, у*  игроков:

х* = 1,   у* = 0    при     k₁ > 0,  k₂ > 0;            х* = 0,   у* = 1  при   k₁ < 0,  k₂ < 0;

 0 ≤   х*   ≤ 1,   0 ≤  у*  ≤1    при    k₁ =  k₂ = 0.                   (7.5)

          7.2. Оптимальность по Парето. Если коэффициенты  k₁, k₂  имеют разные знаки, то точка максимума одной  функции выигрыша (7.4) становится точкой минимума другой функции, и здесь требуется другое определение решения задачи.

        Воспользуемся определением решения задачи (7.3), предложенным известным экономистом и социологом Вильфредо Парето (1848 – 1923). Назовем точку  s*  из отрезка [-1,1]  оптимальной по Парето, если для любой другой точки  s  этого отрезка система неравенств

  Н₍₁₎ ( s) ≥ Н₍₁₎ ( s*) ,    Н₍₂₎ ( s) > Н₍₂₎ ( s*)

или

Н₍₁₎ ( s) > Н₍₁₎ ( s*) ,                   Н₍₂₎ ( s) ≥ Н₍₂₎ ( s*)

несовместна.

          По смыслу не оптимальную по Парето точку  s*  можно улучшить по значению одной из функций выигрыша, не ухудшая значения другой функции. Для оптимальной по Парето точки это сделать невозможно.

        Пусть коэффициенты  k₁, k₂  не равны нулю и имеют разные знаки. Если  s* - произвольная оптимальная по Парето точка из отрезка  [-1,1], то в соответствии с ее определением и видом (7.4) функций выигрыша неравенства

k₁ s  ≥  k₁ s*,           k₂ s  >  k₂ s*                               (7.6)

или

k₁ s  >  k₁ s*,           k₂ s ≥  k₂ s*                               (7.7)

не совместны при любом  s,   -1 ≤  s  ≤ 1.  Рассмотрим подробнее неравенства (7.6). В каждом из двух возможных случаев   ( k₁ < 0,  k₂ > 0  или  k₁ > 0,  k₂ < 0)  они принимают противоречивый вид  ( s ≤ s*,  s > s*  или  s ≥ s*,  s < s*). То же справедливо и для неравенств (7.7). Следовательно, в задаче (7.4) любая точка  s*  из отрезка  [-1,1]  оптимальная по Парето.

          7.3. Метод идеальной точки. Введенное определение оптимальности по Парето для рассматриваемого случая оказалось не вполне эффективным. Оно не позволило выделить из исходного множества допустимых точек более узкое подмножество предпочтительных точек. Было бы естественно попытаться ввести на множестве оптимальных по Парето точек новое более сильное отношение предпочтения, которое давало бы приемлемое решение задачи. Его можно задать разными способами, и с одним из них, предложенным Купмансом, мы сейчас и познакомимся.

          Пусть по-прежнему коэффициенты   k₁, k₂   функций (7.3) отличны от нуля и имеют разные знаки. Составим из функций выигрыша (7.4) векторную функцию выигрыша

  Н( s) = ( Н₍₁₎ ( s),  Н₍₂₎ ( s)) = ( k₁ s,  k₂ s)                                      (7.8)

с  областью определения  -1 ≤ s ≤ 1. Областью ее значений служит отрезок прямой  AB  на вспомогательной « критериальной» плоскости переменных  t₁, t₂ .  На рис 7.1 отрезок  AB   изображен для случая   k₁ > 0,   k₂ < 0.  

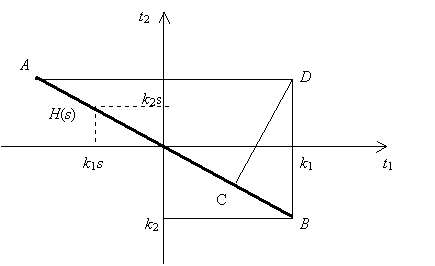
Рис. 7.1. Отрезок прямой  AB – область значений векторной функции (7.8)

         Как видно из приведенного рисунка, наибольшее значение первой и второй функций выигрыша равно  k₁  и  - k₂  соответственно. Точка  D = ( k₁, - k₂), отвечающая максимумам функций выигрыша, была бы идеальным решением задачи. Но, к сожалению, она  не лежит в области значений векторной функции выигрышей и, следовательно, не имеет прообраза на отрезке  -1 ≤ s ≤ 1.

          Найдем ближайшую к «идеальной» точке  D  точку  C   отрезка  AB. Ее координаты и примем за «максимальные» значения функций выигрыша, а соответствующее значение  s* - за искомую точку «максимума», т. е. за решение задачи (7.3).

          Очевидно,  C  есть основание перпендикуляра  CD, опущенного из точки  D  на прямую  AB. Поскольку прямая   AB  имеет угловой  коэффициент  k₂/ k₁ ,  то угловой коэффициент перпендикулярной прямой  CD  равен  - k₁/ k₂. Записав уравнения прямых  AB  и  CD

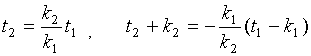
 и решив их совместно, найдем координаты точки C:

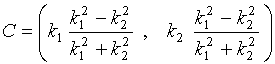.                             (7.9)

Точки (7.8) и  (7.9) совпадают при  s = s*, если принять

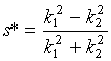.                                           (7.10)

Отсюда и из (7.3), (7.2) получим систему условий для искомых стратегий х*, у*  игроков:

         ( k₁ > 0,  k₂ < 0).           (7.11)

Точно так же в случае  k₁ < 0,  k₂ > 0  будем иметь

      ( k₁ < 0,  k₂ > 0).          (7.12)

          Итак, решение игры «борьба за рынки»  дается формулами (7.5), (7.10) - (7.12).

          7.4. Трактовка и анализ решения. Решения (7.5), (7.10) - (7.12) зависят от исходных данных – коэффициентов  k₁  и  k₂. Если коэффициенты имеют одинаковые знаки, т. е.

k₁ k₂ = ( k₁₁ – k₁₂) ( k₂₂ – k₂₁) > 0,

то каждая компания имеет свой предпочтительный по доходности рынок, на который и направляет всю свою продукцию. Это случаи взаимовыгодного дележа рынков.

            Решения (7.10), (7.11) отвечают коэффициентам разных знаков, т. е.

k₁ k₂ = ( k₁₁ – k₁₂) ( k₂₂ – k₂₁) < 0.

         В этих случаях экономические интересы компаний сосредоточены на одном рынке с наиболее высокой доходностью. При  k₁ ≠ k₂  в соответствии с (7.10), (7.11) имеем  х* - у* ≠ 0, следовательно, доход одной компании сопровождается убытком другой. Это случаи не взаимовыгодного дележа рынков. Поскольку  < 1, то условия (7.11), (7.12) совместны и множество ситуаций  ( х*, у*)  образуют отрезки прямых, лежащих в квадрате (7.2). Оптимальные стратегии, как видно, не единственные, хотя функции выигрыша на них имеют одни и те же значения.

        При  =   по формулам (7.10) – (7.12) получим   s* = 0,  х* = у*. Это случаи безразличия компаний к дележу рынков. При одинаковом распределении продукции между рынками  они не имеют дохода или убытка.

         Оставшиеся случаи  k₁ = 0,  k₂ ≠ 0  и  k₁ ≠ 0,  k₂ = 0  рекомендуем читателю разобрать самостоятельно, используя уже известные решения.

         Полезно обратить внимание на одно важное обстоятельство. Решение игры методом Купманса зависит от того, как определено расстояние от идеальной точки до области значений векторной функции выигрышей. Если, например, меру близости между точками  Н( s)  и  D  на критериальной плоскости определить как «взвешенную» сумму квадратов разностей координат с неотрицательными весами  α₁ , α₂ , то требование ее минимизации приводит к задаче на условный экстремум:

α₁( k₁ s - k₁)² + α₂( k₂ s + k₂)²    → min,      -1 ≤ s ≤ 1.

Ее решение

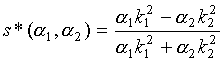
существенно зависит от выбора весов  α₁, α₂. Придавая им различные неотрицательные значения, получим множество решений. Они соответствуют различным положениям точки  Н( s*( α₁, α₂))  на прямой  АВ. Среди решений есть откровенно «эгоистические» ( α₁ = 1, α₂ = 0  или   α₁ = 0, α₂ = 1) и неожиданно «альтруистическое» ( α₁ = k₁^-2, α₂ = k₂^-2). В эгоистических решениях  s*(1,0) = 1   или  s*(0,1) = -1, т. е. одна компания получает максимальный доход, а другая - максимальный убыток. В альтруистическом решении  ( s*( k₁^-2, k₂^-2) = 0) компании довольствуются нулевыми доходами, не причиняя друг другу убытков.

          Широкий спектр решений игры дает хорошую возможность для поиска компромисса. Со способами его нахождения мы познакомимся позже в курсе теории игр.

Вопросы и упражнения

1. В обозначениях  п. 7.3  определим   на  критериальной  плоскости  конус K_H ( s) неравенствами  t₁ ≥ Н₍₁₎ ( s),     t₂ ≥  Н₍₂₎ ( s). Покажите, что точка  s*  из отрезка [-1,1] будет оптимальной по Парето в том и только в том случае, если область значений функции  Н (отрезок  АВ  на рис. 7.1) имеет с конусом  K_H ( s*)  единственную общую точку  Н( s*).

2. Изменим в постановке задачи (7.1), (7.2) вид функций выигрыша, полагая

  Н₁( х, у) =  k₁ mах {0, х – у},   Н₂( х, у) =  k₂ ( х – у),

         где   k₁, k₂ – положительные коэффициенты. Найдите решение задачи.

Будет ли решение задачи в упражнении 2 оптимальным по Парето?

3. Определим расстояние между двумя точками критериальной плоскости: 1) как максимальную по модулю разность - и   2) как сумму модулей разностей соответствующих координат точек. Найдите точку отрезка  АВ  (рис. 7.1), ближайшую к идеальной точке D = ( k₁, - k₂).

4. Можно ли дать введенным в упражнении 4 расстояниям (и методу идеальной точки) экономическую интерпретацию?